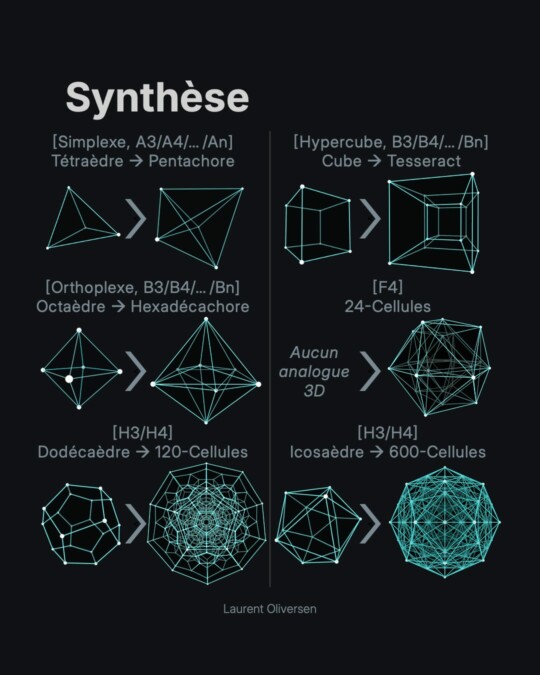
Une histoire de polytopes
La géométrie quadridimensionnelle est la plus riche en “polytopes” (généralisation des polygones/polyèdres) réguliers, convexes et finis.
J’exclus les dimensions 1 et 2 qui sont dégénérées et en tolèrent une infinité.
En 4D, on les appelle les polychores (“plusieurs cellules”).
- Point = 0-polytope
- Segment = 1-polytope
- Carré = 2-polytope = polygone
- Cube = 3-polytope = polyèdre
- Tesseract = 4-polytope = polychore
- Penteract (5-cube) = 5-polytope
- …
- Dekeract (10-cube) = 10-polytope
Principe de réduction dimensionnelle
Mais en fait, les polychores de ce carrousel sont-ils en 3D ?
En effet, on n’a nul autre choix que de projeter les polytopes en 3D ou 2D pour analyser leur silhouette.
C’est un peu comme faire les radio d’un corps humain : on perd une partie de l’information, mais on révèle une structure inaccessible à l’œil.
Pratiquement tous les modèles d’intelligence artificielle ont recours à ces techniques de “réduction dimensionnelle” : ACP, ACM, auto-encoders, embeddings…
Cela permet de réduire le nombre de variables à traiter (et donc de réduire la complexité algorithmique), mais aussi de faciliter les phases exploratoires en visualisant les corrélations et multi-colinéarités.
Dans le carrousel, je montre une projection particulière : le polygone de Petrie. C’est une projection plane globale qui ne favorise aucune face ni aucune arête. Elle montre en particulier l’enveloppe extérieure d’un polytope sous la forme d’un polygone régulier. C’est une photo 2D (on parle de projection orthographique) assez spectaculaire dans la mesure où elle démontre le caractère hautement symétrique de ces objets, pourvu qu’on choisisse les bons angles de projection.
Cas particulier des dimensions N > 4
La richesse des formes s’appauvrit (trop de contraintes spatiales) : on ne retrouve que les simplexes, hypercubes et orthoplexes.
Il existe bien sûr d’autres polytopes, mais ils ne sont plus réguliers, convexes et finis. Ils sont donc “moins symétriques” et “moins esthétiques”.
Le lien avec Platon
Nombreux sont les scientifiques de l’Antiquité à avoir étudié les solides de Platon : Pythagore, Euclide, etc.
On peut y voir une fascination pour leur esthétique particulière. Platon associait chaque polyèdre régulier convexe à un élément :
- Tétraèdre : pointe —> Feu
- Cube : stabilité —> Terre
- Octaèdre : légèreté —> Air
- Icosaèdre : quasi-sphère —> Eau
- Dodécaèdre : divine proportion (via le pentagone dont la géométrie repose sur le nombre d’or) —> Cosmos / Quintessence
Pour ma part, les polychores m’évoquent la symétrie et la complémentarité des pièces d’un échiquier :
- Pentachore : simplicité —> Pion
- Tesseract : orthogonalité —> Tour
- Hexadécachore : dual du tesseract (pyramide) = diagonales —> Fou
- 24-Cellules : hybridation spéciale du tesseract et de l’hexadécachore —> Cavalier
- 120-Cellules : structure fondamentalement pentagonale = mouvement des “5 autres” —> Dame
- 600-Cellules : dual du 120-Cellules et ultra-densité = mouvement contraint —> Roi
Et s’il faut trouver le 6ème élément (pour honorer le 24-Cellules), j’ai plusieurs candidats : la foudre (voire le plasma), la lumière ou les ténèbres…
Fiche technique de ces monstruosités géométriques
| Polytope | Groupe de Coxeter | 🔵 Sommets | 📏 Arêtes | 🟪 Faces | 🧱 Cellules | 🧊 Type de cellules | 🔶 Type de faces | 🔗 Arêtes par sommet | ✴️ Figure de sommets |
|---|---|---|---|---|---|---|---|---|---|
| Pentachore (5-cellules) | A4 | 5 | 10 | 10 triangles | 5 tétraèdres | Tétraèdres | Triangles équilatéraux | 4 | Tétraèdre |
| Tesseract (8-cellules) | B4 | 16 | 32 | 24 carrés | 8 cubes | Cubes | Carrés | 4 | Tétraèdre |
| Hexadécachore (16-cellules) | B4 | 8 | 24 | 32 triangles | 16 tétraèdres | Tétraèdres | Triangles équilatéraux | 6 | Octaèdre |
| Icositétrachore (24-cellules) | F4 | 24 | 96 | 96 triangles | 24 octaèdres | Octaèdres | Triangles équilatéraux | 8 | Cube |
| Hécatonicosachore (120-cellules) | H4 | 600 | 1200 | 720 pentagones | 120 dodécaèdres | Dodécaèdres | Pentagones réguliers | 4 | Tétraèdre |
| Hexacosichore (600-cellules) | H4 | 120 | 720 | 1200 triangles | 600 tétraèdres | Tétraèdres | Triangles équilatéraux | 12 | Icosaèdre |
| Tétraèdre | A3 | 4 | 6 | 4 | — | — | Triangles équilatéraux | 3 | Triangle équilatéral |
| Cube (Hexaèdre) | B3 | 8 | 12 | 6 | — | — | Carrés | 3 | Triangle rectangle isocèle |
| Octaèdre | B3 | 6 | 12 | 8 | — | — | Triangles équilatéraux | 4 | Carré |
| Dodécaèdre | H3 | 20 | 30 | 12 | — | — | Pentagones réguliers | 3 | Triangle isocèle (angles 108°) |
| Icosaèdre | H3 | 12 | 30 | 20 | — | — | Triangles équilatéraux | 5 | Pentagone régulier |