Certains parlent de révolution, voire de suprématie quantique. Mais pour démêler le vrai du faux, il faut revenir à la promesse de l’informatique quantique. Et cette promesse, c’est de résoudre certains problèmes beaucoup plus vite que les ordinateurs classiques. On parle de réduction drastique de la complexité algorithmique. C’est-à-dire que le nombre d’opérations à effectuer pour trouver la solution à un problème augmente bien moins vite qu’avec des ordinateurs conventionnels. Pour certains problèmes, cela représente des facteurs d’accélération considérables (des années de calcul deviennent des minutes).

Sur le papier, de belles promesses. Dans la pratique, beaucoup de bullshit, car les ordinateurs quantiques sont encore instables et sujets à beaucoup d’erreurs. Mais cela s’améliore mois après mois.

Pour t’en convaincre, voici une illustration simplifiée du fonctionnement de l’un des premiers algorithmes quantiques de l’histoire : l’algorithme de Deutsch-Jozsa.

Problème

L’objectif : on a une fonction mystère F qui prend en entrée 0 ou 1, et qui retourne en sortie 0 ou 1.

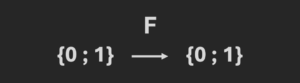
Cette fonction peut être constante, F(0) = F(1) ou non constante F(0) ≠ F(1). Le but est justement de savoir si F est constante ou non.

Analogie classique

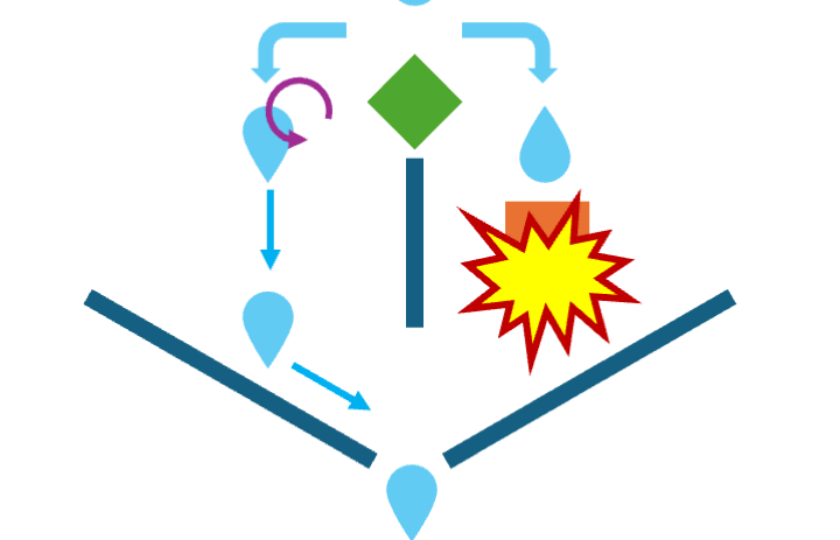
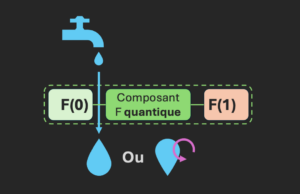
On va faire l’analogie d’un ordinateur classique en imaginant un composant électronique qui simule le fonctionnement de F.

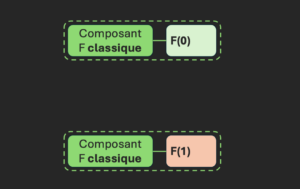
On suppose que ce composant fictif agit sur de l’eau. Pourquoi cette analogie ? Parce que ce sera plus simple quand on basculera à l’échelle quantique.

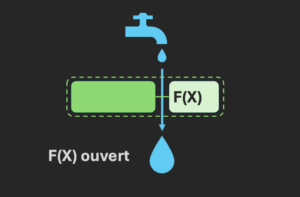
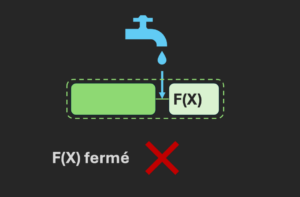
Le composant agit de deux manières : soit il laisse passer les gouttes, soit il les bloque (cela permet de coder 0 ou 1 en sortie).

Pour déterminer si la fonction est constante, on va simplement tester le comportement des configurations F(0) et F(1). Sur le schéma suivant, la goutte de gauche appelle F(0) et celle de droite F(1).

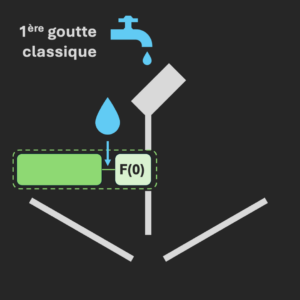
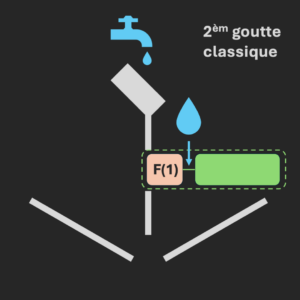
Et il suffit de comparer ce qui sort du circuit dans les deux cas. Si au global, on observe deux gouttes ou rien du tout, alors la fonction est constante. Si on n’observe qu’une seule des deux gouttes, la fonction n’est pas constante. Plutôt simple.

Analogie quantique

Désormais, on imagine que la goutte d’eau passe à l’échelle atomique et se dote de propriétés quantiques. Trois hypothèses sont nécessaires pour transposer l’analogie précédente :

Déphasage

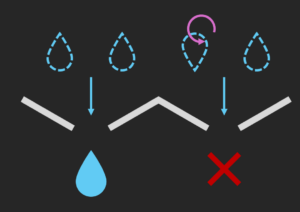
Désormais le composant se comporte ainsi : soit il laisse passer la goutte, soit il la “retourne” (goutte orientée “pointe en bas”). Ce retournement est une métaphore du déphasage des photos.

Superposition

Quand une goutte d’eau quantique arrive à une bifurcation, elle emprunte virtuellement tous les chemins qui s’offrent à elle. Attention, ce n’est pas un vrai dédoublement, mais une répartition de sa probabilité de présence. C’est pour cela qu’on parle ici de goutte “virtuelle”.

Interférences

Deux gouttes d’eau virtuelles orientées de la même manière peuvent se recombiner (et une goutte d’eau réelle devient alors observable). En revanche, deux gouttes tête-bêche (orientées différemment) interfèrent et s’annihilent : aucune goutte ne peut alors être détectée en sortie.

Mise en pratique

Maintenant que l’on a ces trois hypothèses, on place le composant quantique transversalement au parcours précédent.

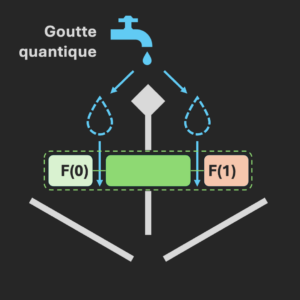
Une goutte d’eau quantique emprunte virtuellement les deux branches et appelle les deux valeurs de la fonction simultanément.

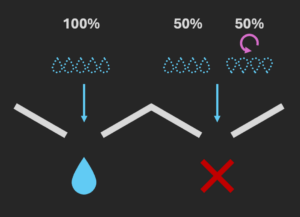
Ainsi, si la fonction est constante, alors les gouttes virtuelles seront orientées de la même manière et pourront se recombiner (on observe une goutte en sortie). Sinon, les gouttes seront tête-bêche et s’annihileront : aucune goutte visible en sortie.

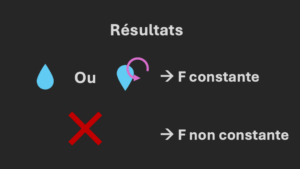
Dans un cas classique, on a eu besoin de deux gouttes et on a dû effectuer deux calculs différents consécutifs. En quantique, on a utilisé une unique goutte et il s’agit d’un unique appel de fonction : un seul calcul effectué sur un état superposé (deux chemins virtuels).

Finalement, on a fait une opération au lieu de deux. Un avantage bien modeste, pourrait-on dire. Mais voici une extension plus intéressante.

Cas général

On a une fonction F qui prend N variables binaires (0, 1) en entrée et renvoie un binaire en sortie. On cherche à savoir si F est constante ou “équilibrée” (50 % des sorties valent 0 et 50 % valent 1).

Prenons l’exemple de N = 1000.

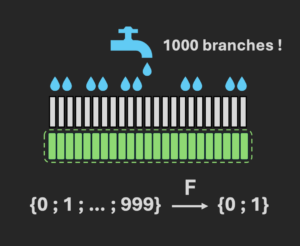
Dans un algorithme classique, il faut appeler la fonction sur chacune des 1000 variables d’entrée (que l’on numérote de 0 à 999).

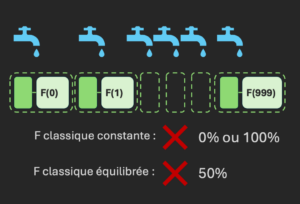
Avec de la chance : en prenant juste deux entrées (ex : F(0) et F(1)), si les valeurs sont différentes, c’est que la fonction n’est pas constante, donc équilibrée. Mais dans le pire des cas, il va falloir tester la (moitié + 1) variable pour conclure avec certitude.

En effet, supposons que F(0) = F(1) = … = F(499), alors on ne sait toujours pas si la fonction va rester constante ou si les sorties commencent à changer à partir de la 500-ème entrée. Mais si F(499) = F(500), alors on peut conclure qu’elle est constante.

Pour un ordinateur quantique, la fonction est constante si le composant agit sur les gouttes virtuelles de la même manière, et équilibrée s’il retourne une goutte sur deux.

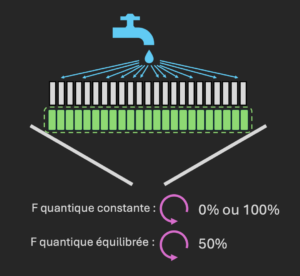
Désormais, les interférences agissent ainsi de la façon suivante : si les 1000 gouttes virtuelles sont orientées de la même manière, elles se recombinent. Si 50 % des gouttes sont orientées “pointe en bas”, alors les 1000 gouttes s’annihilent.

La goutte quantique explore les 1000 branches en parallèle (encore les merveilles de la superposition). Une fois encore, il suffit d’une unique goutte et d’un seul calcul pour conclure : si une goutte apparaît en sortie, c’est que la fonction est constante.

Notons qu’au-delà de son caractère éducatif, l’algorithme de Deutsch-Jozsa n’a aucune application pratique. En revanche, il a servi d’inspiration à d’autres algorithmes qui ont une réelle utilité (dans le domaine du chiffrement ou de la résolution d’équations), notamment dans certains traitements d’intelligence artificielle. Enfin, contrairement à cet algorithme, toutes les accélérations ne sont pas exponentielles…